机器学习笔记(一)
机器学习笔记(一)
在油管看了 Andrew Ng 的课,发现真正的专家就是能够将晦涩难懂的知识结合生活的趣事讲得有滋有味,丝毫没有平时听课的那种困乏感,因此有点像追剧一样一连看了好几节,口齿清楚,节奏也把握得当,尽管一节只几分钟,但确实是将知识点讲清楚了,干货满满,在此整理了一些我个人学习的笔记和思考
¶1. 什么是机器学习
两种主要的机器学习:
- 监督学习(supervised learning)
- 无监督学习(unsupervised learning)
监督学习在现实中的应用很广泛
增强学习(reinforcement learning):另一种机器学习算法
了解如何运用工具才是最重要的
¶2. 监督学习
x -> y
input -> output label
从给定的正确答案中学习(即给定x的正确标签y)
算法通过对于正确的x、y搭配学习,最终在只输入x的时候,对于输出y进行预测
| Input(X) | Outout(Y) | Application |
|---|---|---|
| spam?(0/1) | 垃圾邮件过滤器 | |
| audio | text transcripts | 语音识别 |
| English | Spanish | 机器翻译 |
| ad,user info | click?(0/1) | 在线广告 |
| image,radar info | position of other cars | 自动驾驶汽车 |
| image of phone | defect?(0/1) | 目视检查 |
主要算法类型:
①回归算法(Regression):从无限可能中进行预测(e.g. 房价预测)
②分类算法(Classification):有限种可能(e.g. 乳腺肿瘤预测)
¶3. 无监督学习
给定x的时候没有添加标签的y,对于给定的数据集,使用算法找出其中的特点或结构,而不是标记正确的答案
使用算法对于未被标记的数据分成簇(e.g. 谷歌新闻,基因分类,客户分类)
聚类算法(Clustering)
异常检测(Anomaly detection):找到异常的点
降维(Dimensionality reduction)
¶4. Jupyter Notebooks
当前流行的数据科学以及机器学习的工具,可以配合上Numpy、Matplotlib等内容进行数据分析
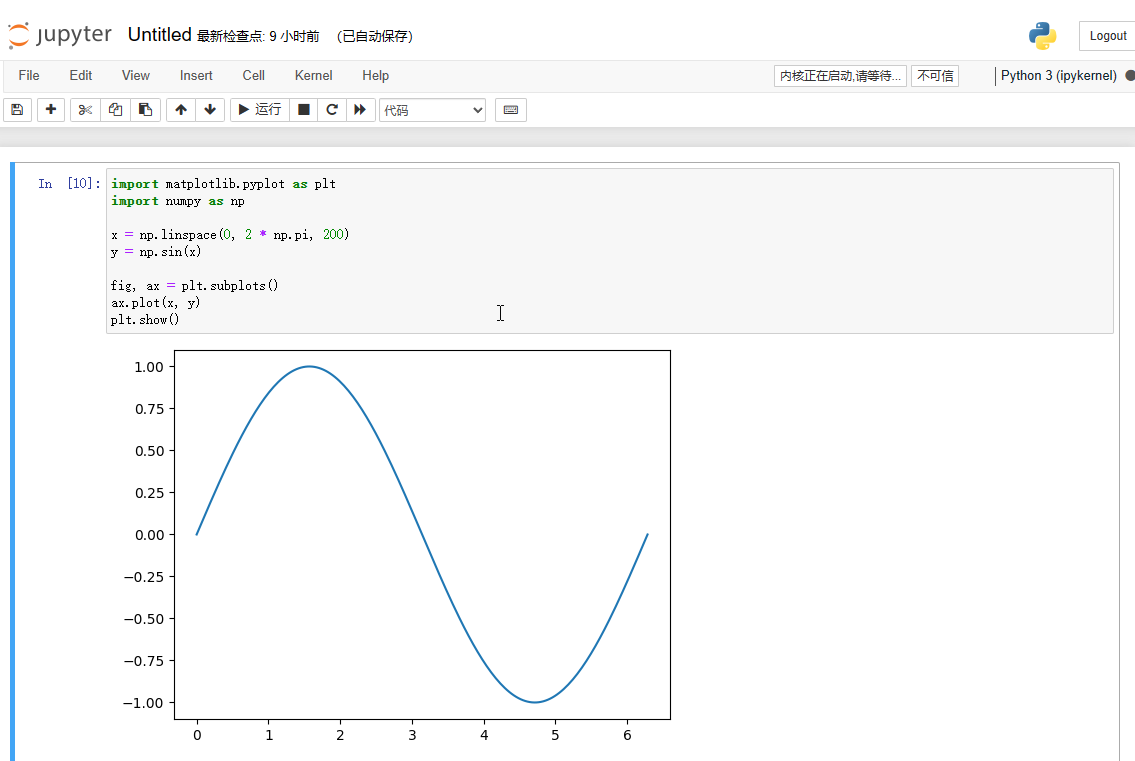
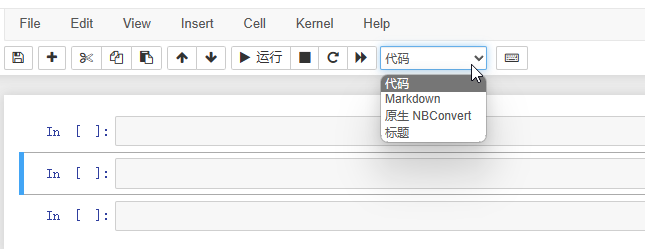
两种Cell,包括Markdown Cell和Code Cell
¶5. 线性回归
线性回归模型
简单了解可以使用线性回归处理的问题
例:根据房屋的大小预测房屋的价格
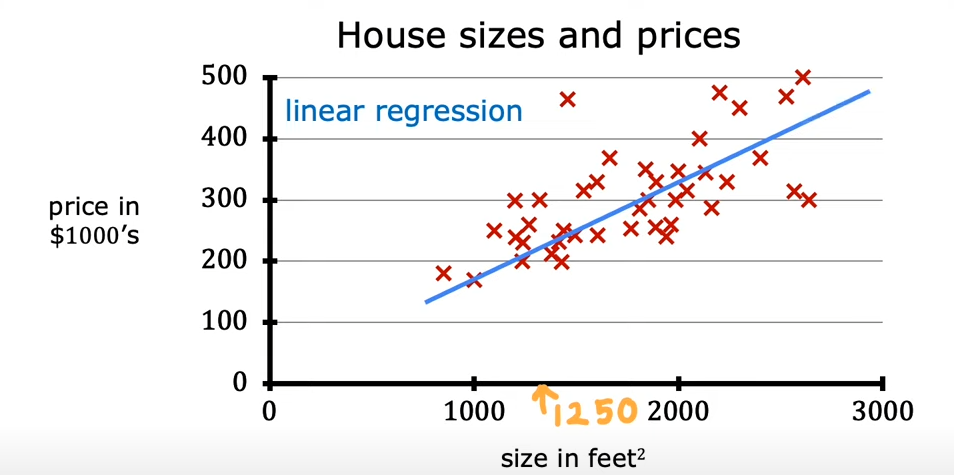
根据数据画出一条直线
这是一种监督学习的模型,事先给出的数据集是正确的答案,即成对的x、y
回归模型是用来预测数字的监督学习模型,处理预测具体数值的回归问题
线性回归模型只是回归模型的一种
另一种最常见的监督学习模型是分类模型,用于预测分类和离散分类
回归和分类最大的区别在于分类只会有少量的可能输出结果,而回归可能有无穷多种结果
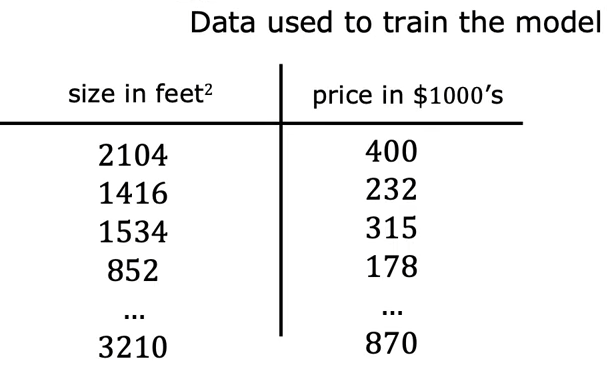
训练集(training set):用于训练模型的数据集
首先通过输入的训练集训练模型,然后模型根据特定的值进行预测
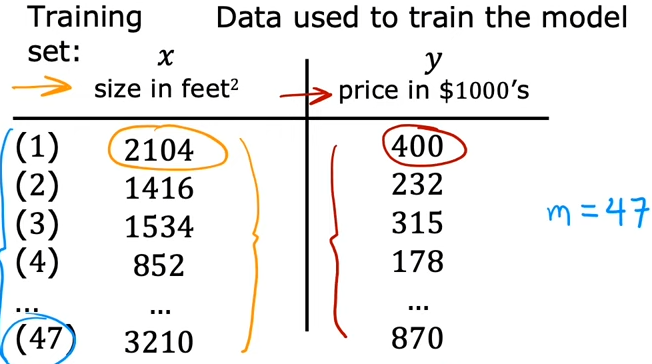
代表输入变量,称为特征(feature)或者输入特征 比如2104
代表输出变量,称为目标 比如400
代表训练样本的总数 这里就是47
(, )表示一个单独的训练样本,比如这里的(2104, 400)
()表示第i个训练样本
比如(2104, 400)可以表示为 (),1代表的其实就是训练集的行
在监督学习中,训练集包含输入的特征以及输出的目标(正确的结果),这些用来喂给训练算法
然后训练算法产生一个函数,使用表示,它的职责是通过输入一个新的,然后预测或者估计一个 ,这个代表的估计值或者预测值
就被称为模型(model),X被称为输入特征,代表真实的目标,直到真正发生才会知道
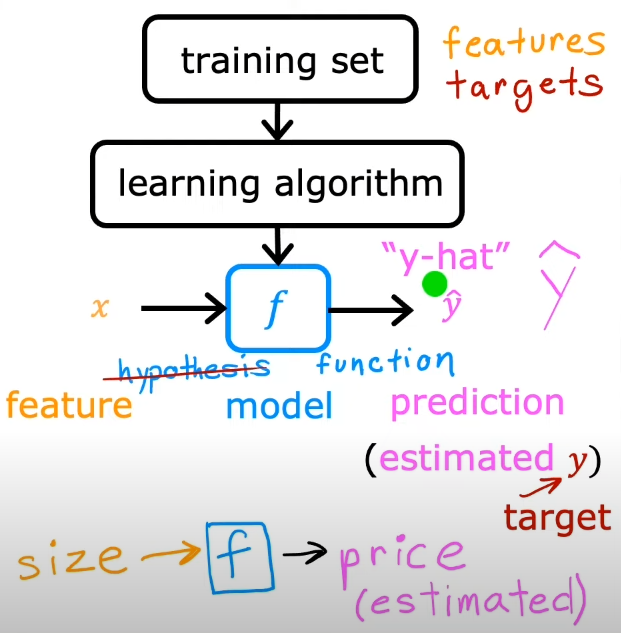
关键问题:怎样表示?
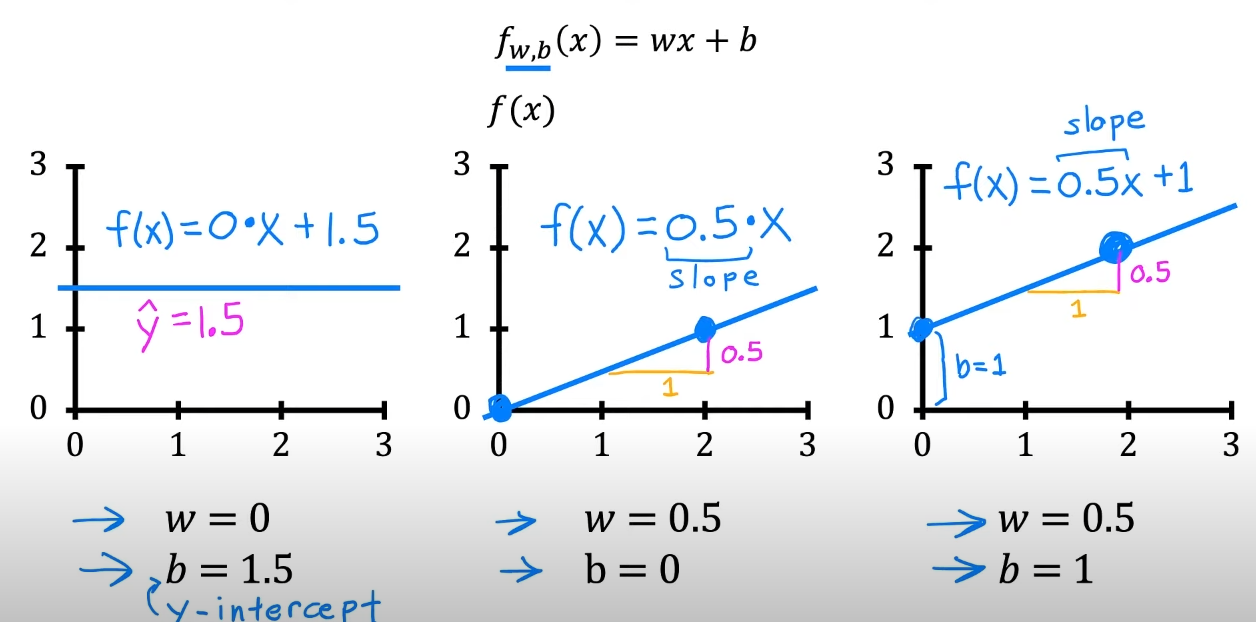
输入不同的,根据和的取值,输出一些的预测值

当前这种接收的的表达,也被称为单变量线性回归(univariate linear regression)
¶6. 成本函数(cost function)
对于这个而言,和可以称为该模型的参数(parameter)
那么,和究竟扮演了什么角色?
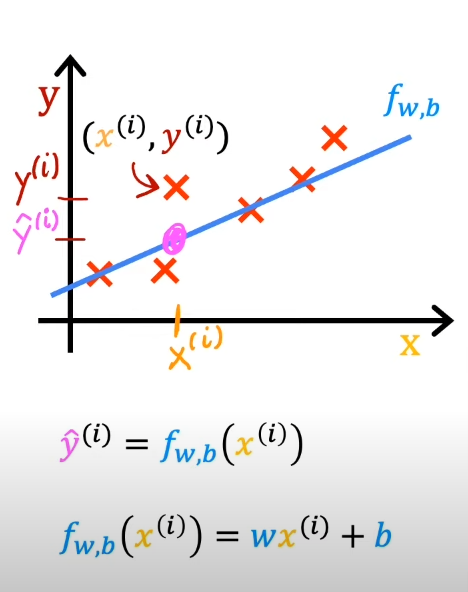
对于训练集而言,里面的任意数据可以使用()表示,那么可以将进行转化
通过模型,我们想要输入具体的,给出目标的预测值,并且使其尽可能接近真实值
对于线性回归来说,可以将进一步表述为:
怎样找到合适的和?这就需要我们构造成本函数了
¶成本函数的构造
-
首先,用 - ,这是求得预测值与真实值之间的误差
-
然后,将的结果求出,这其实是方差
-
然后考虑到要求每一组训练样本的方差,那么需要配合进行表示
-
最终我们将所有的训练样本的方差求和,并且为了数据不会增长过快,再乘上,为了后面计算更简便,再除以2
注意:这里的是训练样本的数量
以上便是成本函数的公式
我们可以再将替换一下
¶成本函数的探索
我们的主要目的就是使得误差尽可能的小
接下来,先从简单的线性回归开始了解
让b = 0,
这样,我们的成本函数可以写成
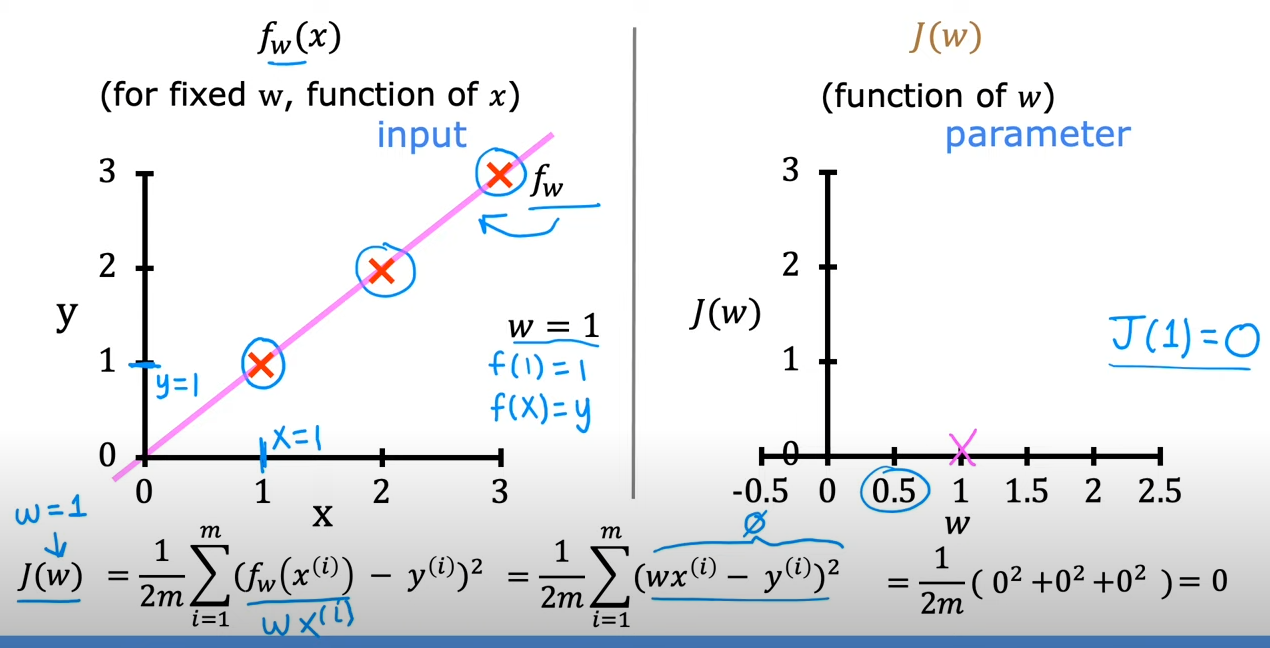
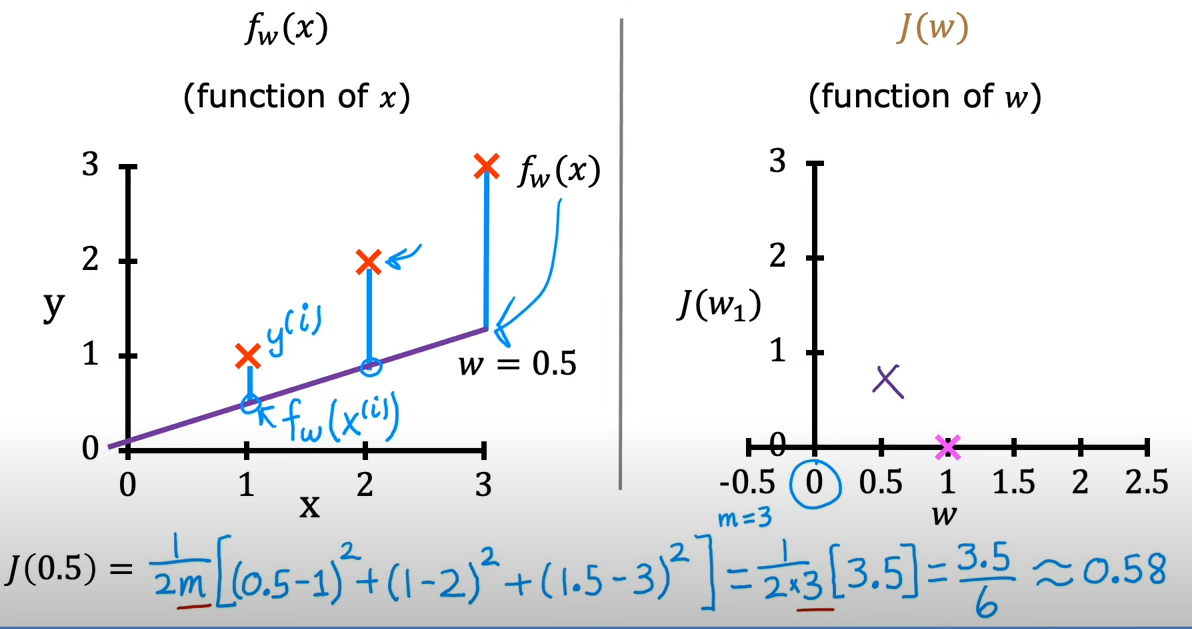
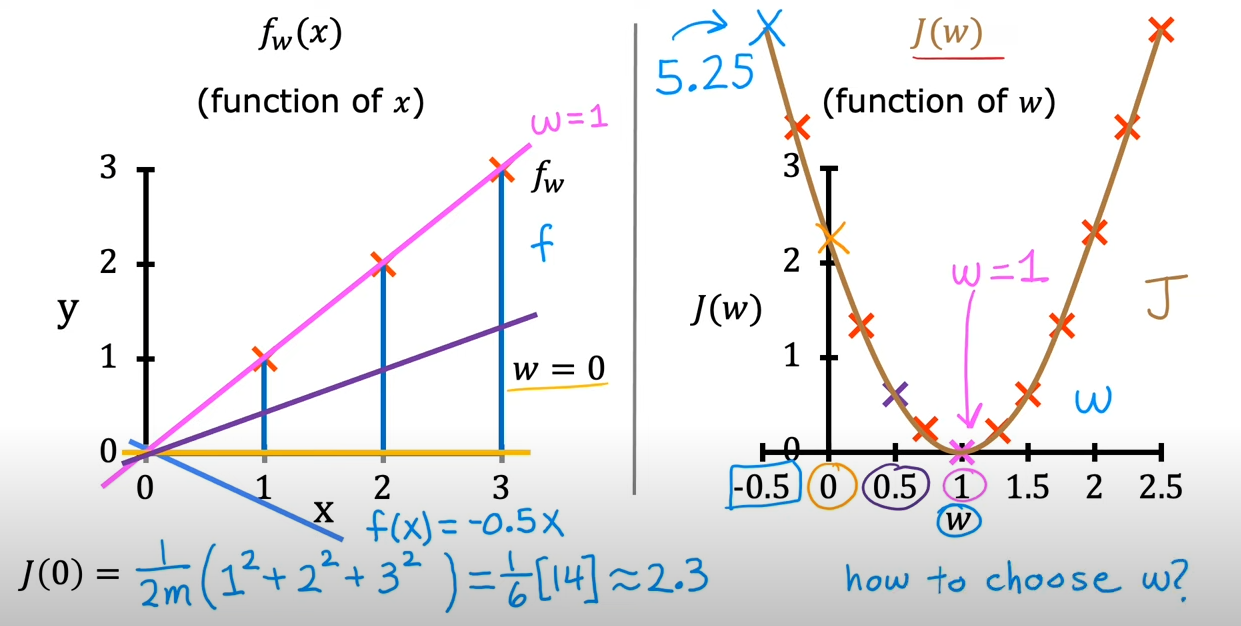
的值取决于,因为在当中,是一个确定下来的值,而会变化,对应输入的有一个与之对应,也就是所谓
而的值取决于
以上描述的便是与之间的联系
¶成本函数可视化
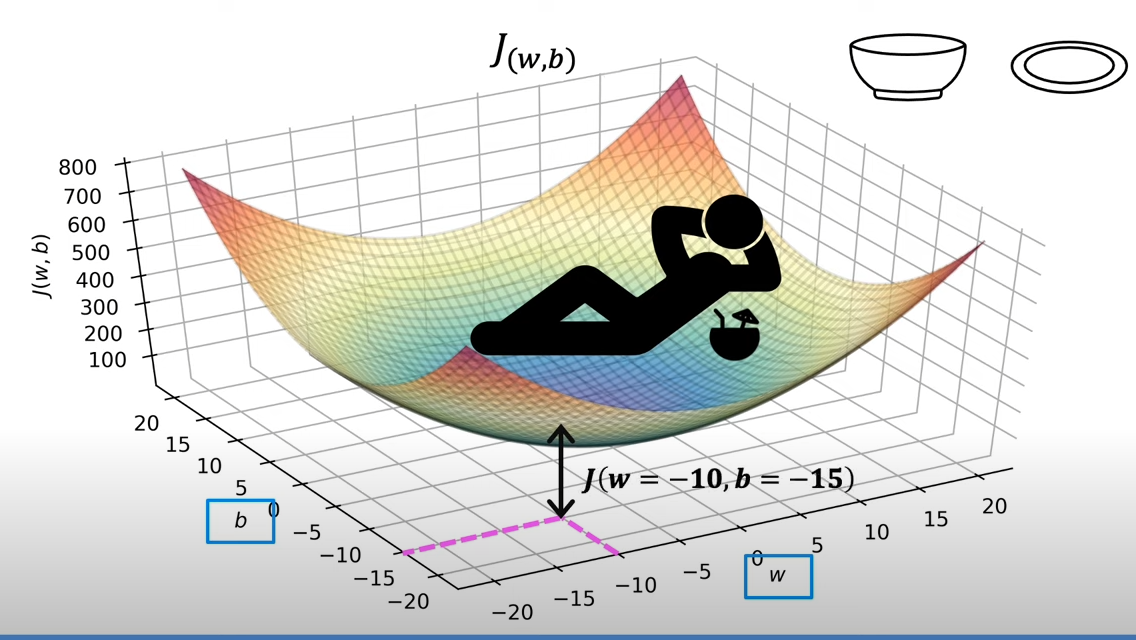
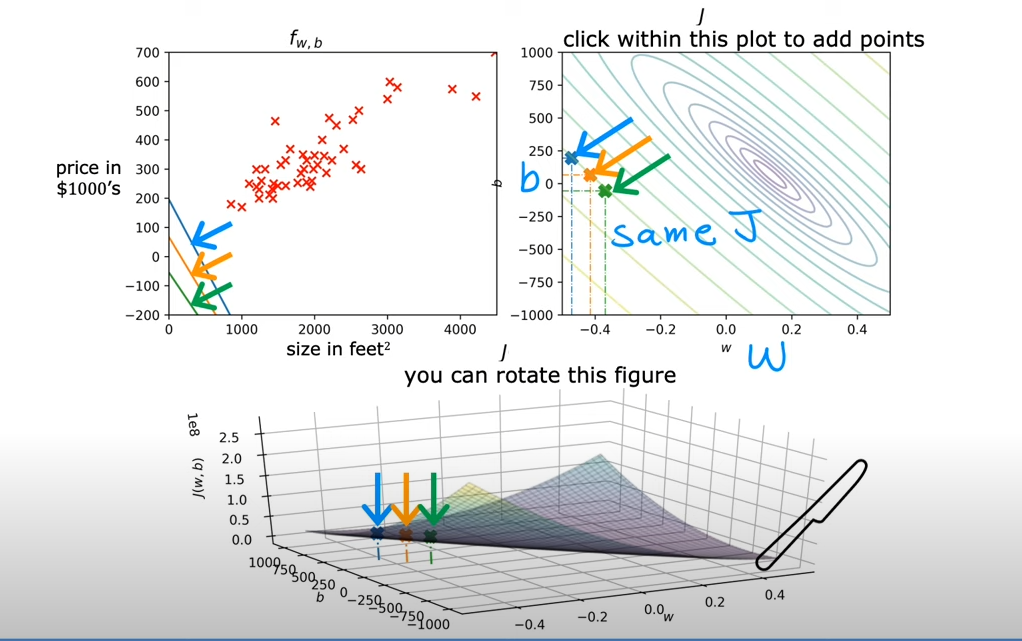
的形状像一个超级碗,根据给定的和变化,因此有和两个轴,体现的是一个三维的图形
可以将的值看做是高度,我们可以将其表示为等高线,在同一条线上的值是相等的
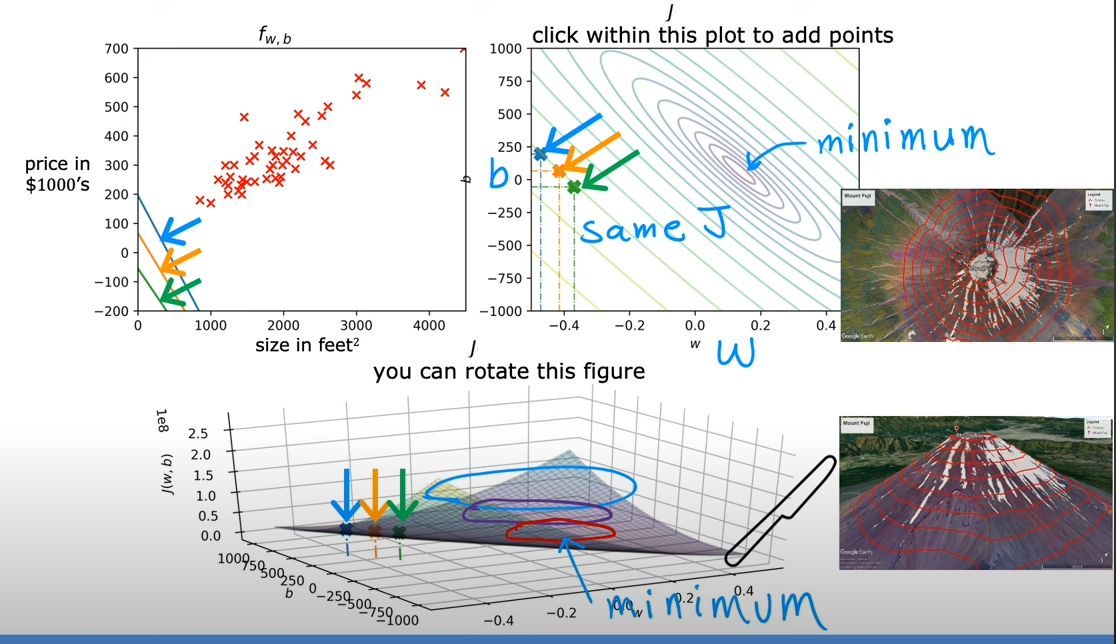
其实,如果需要求最小的,其实取得就是等高线的中心,对应到3D的超级碗上,其实就是碗的底部
¶可视化案例
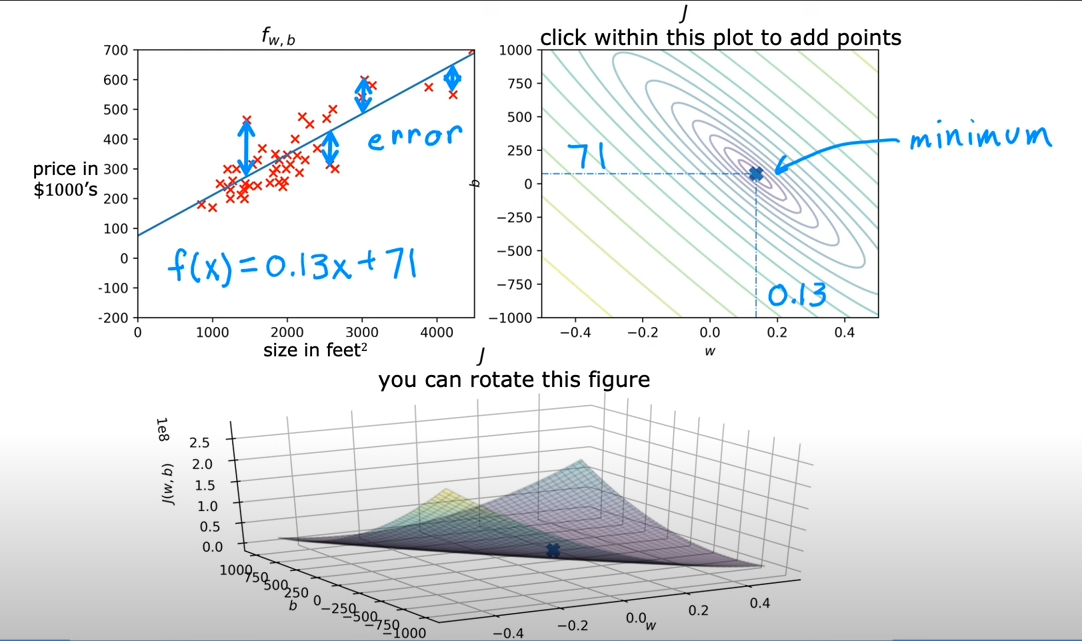
¶7. 梯度下降
梯度下降算法可以用于将任何的函数最小化,而不仅仅是线性回归的成本函数
我们的主要目标是获取的最小值
做法:
-
首先设置初识的和(比如说把它们都设置成0)
-
持续更换和来减小的值,知道我们达到或者接近最小值(因为可能不止一个最小值)
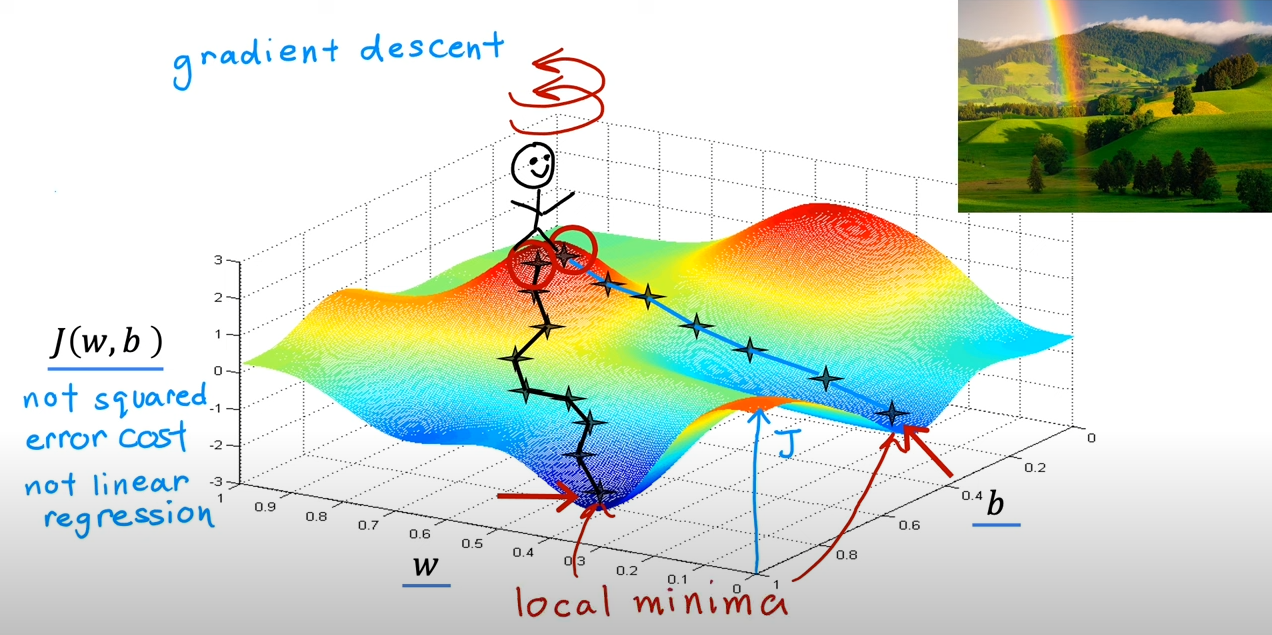
可以想象你人站在山顶的某处,这就是你选定的初始点,然后你需要选择一条下山最快的路
这个时候你原地旋转一圈,找到一个方向(最陡峭),然后迈一步,再重复转一圈,找最陡峭的方向,然后一步步走到一个低谷
但是,如果你开始的位置不同,你可能会沿着另一个方向走进另一个低谷,并且无法发现其他的低谷,那么这是梯度下降算法的一个特点
而这些低谷被称为局部最小值(local minima)
¶实现梯度下降
递推式(=表示赋值)
表示学习率(learning rate),通常是一个0~1之家的正数,用于控制下山的步伐的大小

需要注意的是,和是同时更新的,因此在给和赋值时,二者需要都被更新
¶梯度下降的导数
简化一下,只和相关

在某个点做一条切线,那么计算这个点的正弦,或者说斜率,便是导数的数值了
在上图的方向上,斜率为正,因而减去一个正值会不断变小
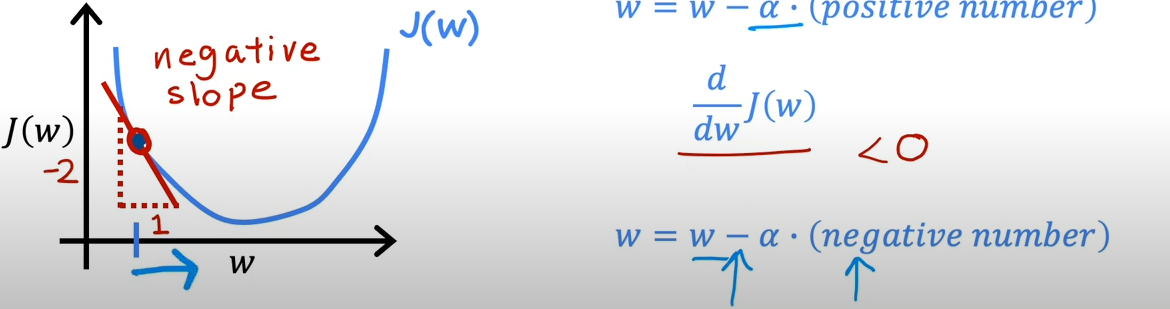
在这个例子里面,取另一个点,此时斜率为负,因而会不断增大
¶梯度下降的学习率
依然沿用先前简化的, 现在我们考虑如果很小会发生什么
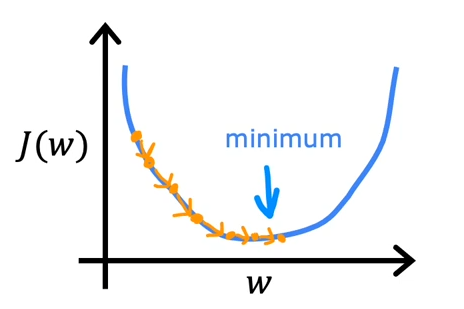
借助和关系的曲线,如果选定某个点,然后一点点,迈着婴儿的步伐,慢慢地下降,那么当然最终是可以到达谷底的,但是这却要耗费相当长的时间
换句话说,梯度的下降非常缓慢

但是如果取值太大,有可能导致一步跨过最小值,这反而会更糟
通过判断导数为0,可以找出局部最小值点
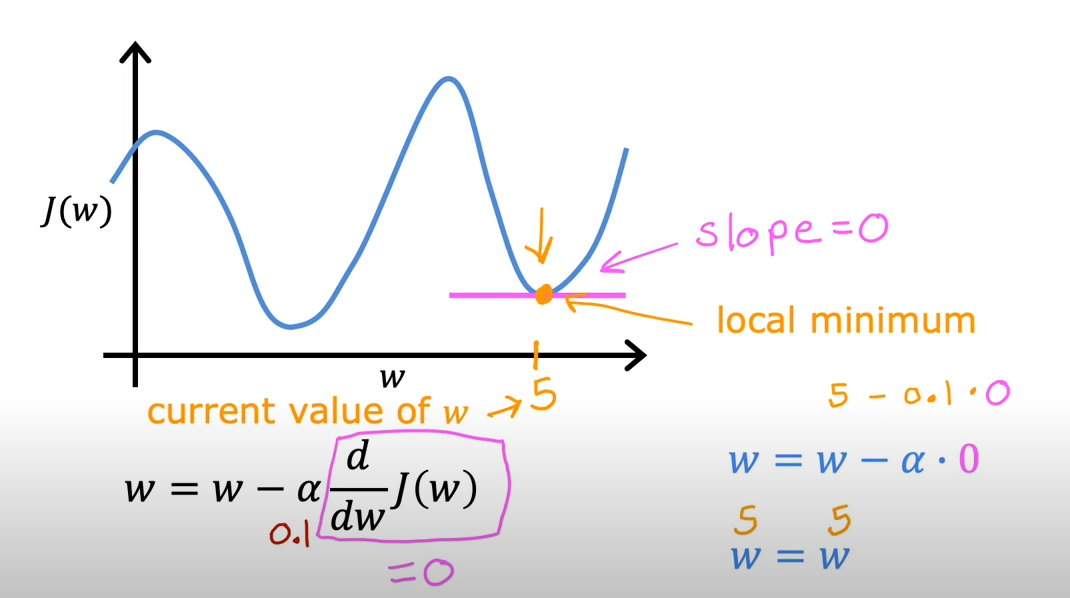
到达这种点时,导数为0,因此的值不再变化
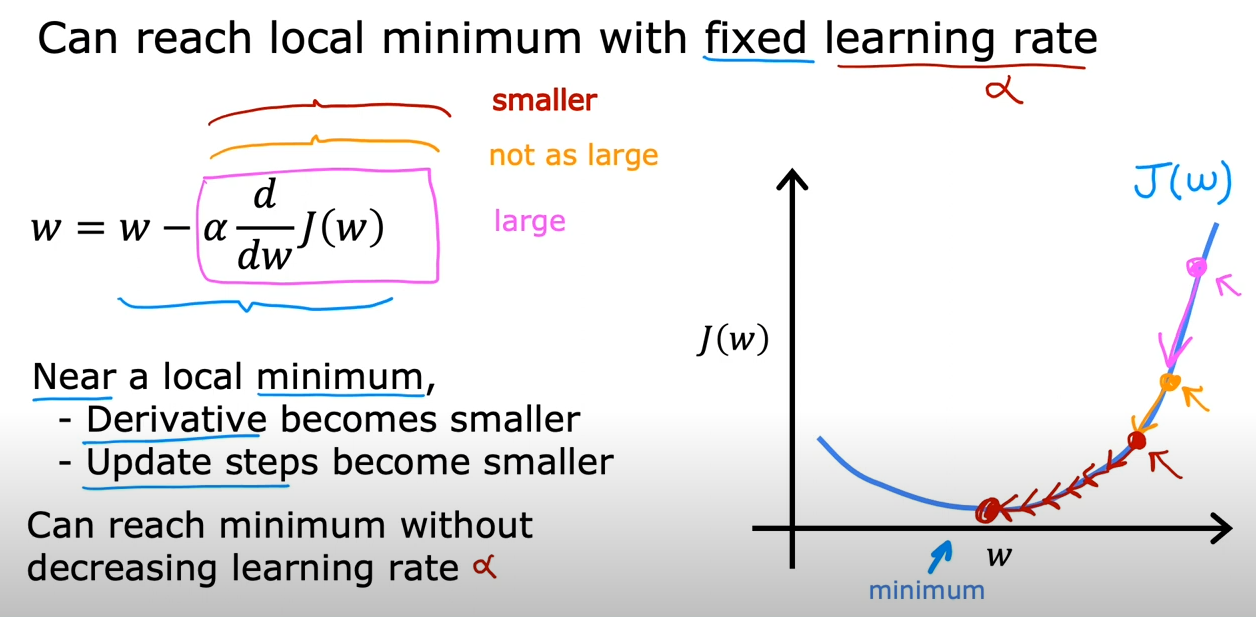
使用固定的学习率,当越来越接近最小值的时候,斜率会越来越小,步子也会越来越小
因此,可以在保持学习率不变的情况下,逐渐接近最小值
¶线性回归的梯度下降

根据先前总结的递推式,将原始的代入进行化简
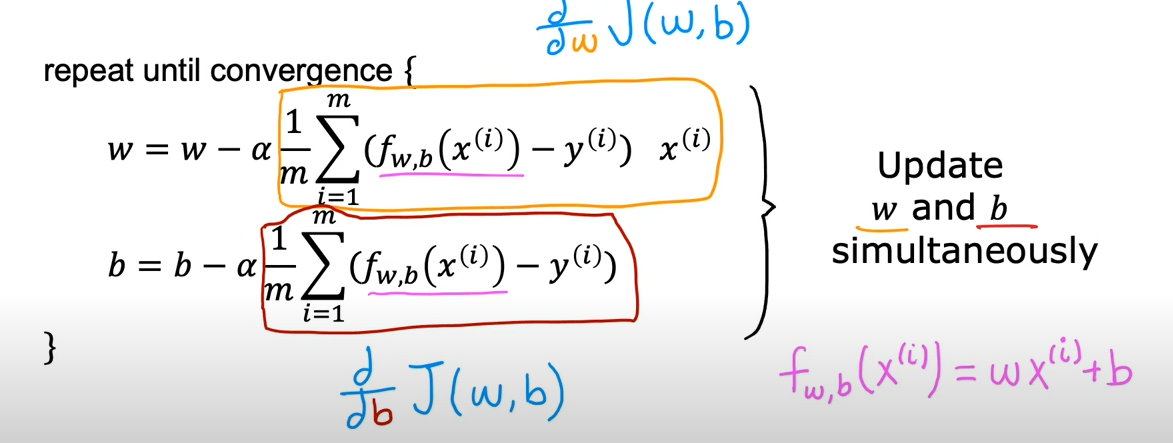
由于线性回归的成本函数是一个凸函数,因此的它的形状是碗状的,只会有一个全局最小值
因此,只要学习率选择恰当,总是能够找到它的最小值
¶应用梯度下降
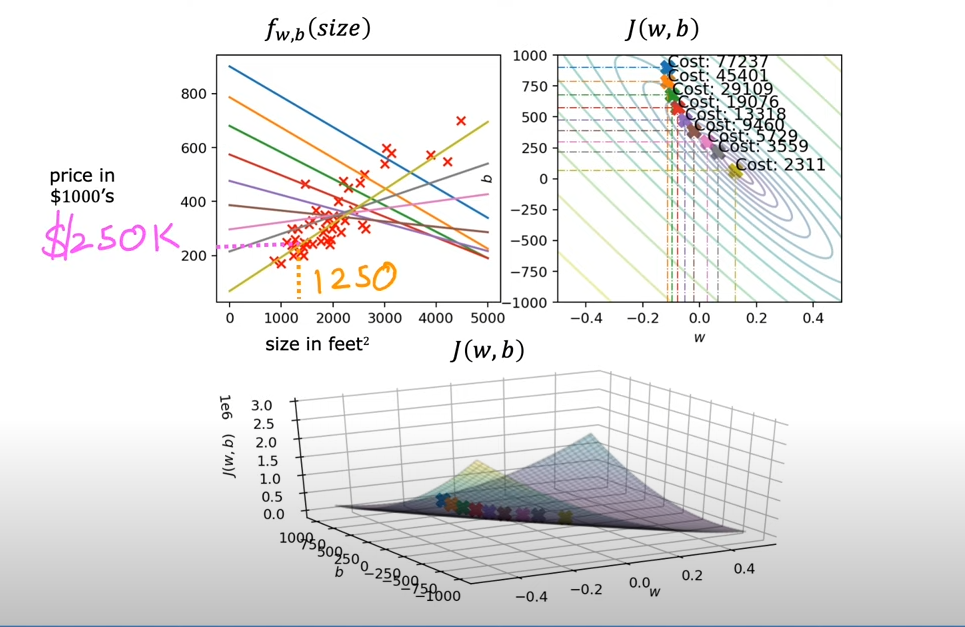
批梯度下降:梯度下降中的每一步都需要检查所有的样本,而不是样本的子集




